Muutama metri aitaa

Kolmannen luokan matematiikka sekoittaa aikuisten päät.

Julkaistu 5.7.2016, kategoriassa Älynväläys

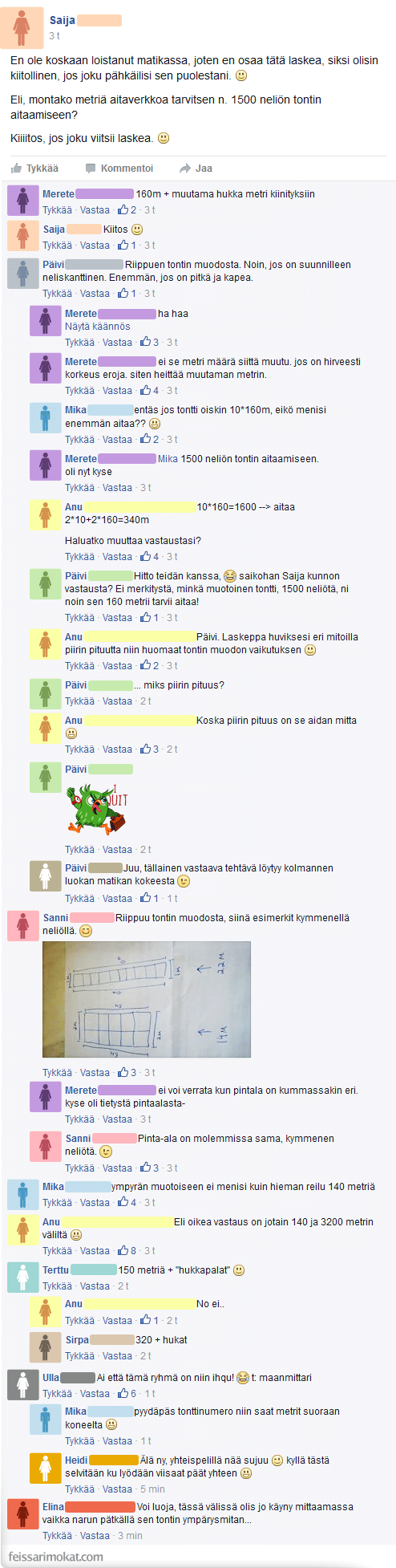
Seuraava
Postiluukusta tipahti shokkilasku. Edellinen
Äitylit asioivat Kelassa ja käyvät gynekologilla.

49 kommenttia

Sargee 5.7.2016 4:13

Tulos: +106 (170 ääntä)

*Facepalm*

Lainaa
Mari 5.7.2016 4:29

Tulos: +283 (303 ääntä)

Miten se sanonta niistä kokeista ja sopasta menikään..?

Lainaa
Paro 5.7.2016 4:42

Tulos: -171 (213 ääntä)

No, olihan se ensimmäinen vastaus periaatteessa oikein

Lainaa
Lyhyt matikka 5.7.2016 5:33

Tulos: +59 (71 ääntä)

Öh.. hyvin meni taas ja silleen

Lainaa
Luu 5.7.2016 7:40

Tulos: +306 (342 ääntä)

Paro: No, olihan se ensimmäinen vastaus periaatteessa oikein
Mitä sanaa kohdasta "riippuu tontin muodosta" et ymmärtänyt?

Lainaa
JKA 5.7.2016 8:42

Tulos: +264 (274 ääntä)

Paro: No, olihan se ensimmäinen vastaus periaatteessa oikein
Käytännössä vastaus saattoi olla oikea, mutta ei ainakaan periaatteessa.

Lainaa
Rampe&Naukkis 5.7.2016 9:37

Tulos: -134 (182 ääntä)

"Huoh" pitäisikö näille opettaa, mikä on neliöjuuri ja neliö? Neliöjuuri ei siis oo kasvi tai neliö ympyrä.

Lainaa
Ryusuzaku 5.7.2016 9:45

Tulos: -83 (121 ääntä)

Todennäköistä että ensimmäinen osuu oikeaan jos miettii näitä suomen tontteja harvemmin on kauhean kapeita ja pitkiä ainakaan.

Lainaa
Heb 5.7.2016 10:02

Tulos: +272 (282 ääntä)

Jos ajatellaan, että tontti on tehty labyrintin muotoiseksi n. 1cm levyisenä siivuna, niin kyllähän tuohon aitaa saa menemään...

Lainaa
KlaaraKotko 5.7.2016 10:08

Tulos: -248 (272 ääntä)

Siis.. Oliko se tossa piirustuksessa vaan tuhrinut sinne sisään kuulakärkikynällä kymmenen neliötä.

Lainaa
EEH 5.7.2016 10:09

Tulos: +112 (146 ääntä)

Pelkää pinta-alal ei kukaa matemaatikko pysty sitä tarkkaa piiriä eli aitamäärää selvittämään. Ihmettelen myös miksei kukaan keskustelun matemaatikoista tajunnut kysyä Saijalta edes sitä tontin muotoa. Joku voisi ottaa nyt tehtäväkseen laskea millä todennäköisyydellä saa laskettua sen tontin piirin oikein jos tietää vaa pinta-alan.

Lainaa
Väsynyt 5.7.2016 10:44

Tulos: +161 (169 ääntä)

Mutta kuinka korkea aita pitää 1500 neliön pihalle laittaa?

Lainaa
E 5.7.2016 11:10

Tulos: +232 (234 ääntä)

KlaaraKotko: Siis.. Oliko se tossa piirustuksessa vaan tuhrinut sinne sisään kuulakärkikynällä kymmenen neliötä.
Ei se varmaan niitä neliöitä sellaisinaan mitannut, kunhan havainnollisti asiaa visuaalisin keinoin.

Lainaa
ssss 5.7.2016 11:31

Tulos: +85 (93 ääntä)

EEH: Pelkää pinta-alal ei kukaa matemaatikko pysty sitä tarkkaa piiriä eli aitamäärää selvittämään. Ihmettelen myös miksei kukaan keskustelun matemaatikoista tajunnut kysyä Saijalta edes sitä tontin muotoa. Joku voisi ottaa nyt tehtäväkseen laskea millä todennäköisyydellä saa laskettua sen tontin piirin oikein jos tietää vaa pinta-alan.
Vähän päälle 0% ajasta saa täysin oikein pelkällä pinta-alalla.

Lainaa
Painoläjä 5.7.2016 11:49

Tulos: +35 (45 ääntä)

ssss: Vähän päälle 0% ajasta saa täysin oikein pelkällä pinta-alalla.

EEH: Pelkää pinta-alal ei kukaa matemaatikko pysty sitä tarkkaa piiriä eli aitamäärää selvittämään. Ihmettelen myös miksei kukaan keskustelun matemaatikoista tajunnut kysyä Saijalta edes sitä tontin muotoa. Joku voisi ottaa nyt tehtäväkseen laskea millä todennäköisyydellä saa laskettua sen tontin piirin oikein jos tietää vaa pinta-alan.
No sä et ainakaan se matemaatikko oo. Mahdollisuus lähestyy nollaa koska mahdollisia vastauksia äärettömästi

Lainaa
x*y 5.7.2016 12:01

Tulos: +89 (109 ääntä)

Olettaen, että tontin muoto olisi suunnilleen suorakulmainen, voidaan aidan pituudelle tehdä lauseke: A(x)= 2*x+2*y koska x*y=1500 ||:x y=1500/x niin A(x)= 2*x+3000/x Nyt täytyy vain sijoittaa x:n paikalle tontin yhden sivun pituus. Esim A(40)=2*40+3000/40=155 tai A(100)=2*100+3000/100=230

Lainaa
Arthur Brown 5.7.2016 12:03

Tulos: +143 (163 ääntä)

Niin, oikeastaan tässä voi antaa vain minimin, joka on noin 140 metriä. Maksimimitta on ääretön, tai no sen verran että avaruuden geometria pysyy vielä jotenkuten järjestyksessä. Jos aidan pituus lähestyy muutamaa miljardia kilometriä, niin aidan massa alkaa jo vaikuttamaan pituusmittaan. Tätä kun jatkaa, niin koko kysymys aidan pituudesta on lähes filosofinen, kun aita ja tontti puristuvat singulariteetiksi. No...oikea vastaus on toki noin 160 metriä (esim. 30 x 50 m tontti).

Lainaa
Laura 5.7.2016 12:10

Tulos: +102 (106 ääntä)

Pintala

Lainaa
Salla 5.7.2016 12:27

Tulos: +77 (89 ääntä)

Huvittavaa, juuri keväällä opeteltiin näitä nelosluokkalaisteni kanssa.

Lainaa
Petkele 5.7.2016 12:55

Tulos: +161 (177 ääntä)

Salla: Huvittavaa, juuri keväällä opeteltiin näitä nelosluokkalaisteni kanssa.
Opitko?

Lainaa
Baa 5.7.2016 13:16

Tulos: -16 (48 ääntä)

Ongelma on se, että haluttua muotoa ei ole annettu. Jos kyseessä kuitenkin on neliö (huomatkaa, että neliö[metri] on myös pinta-alan yksikkö), on sivun pituus neliöjuuri 1600:sta eli 40. Täten aidan koko pituus on 160m, koska 4*40m = 160m. -- Olisi myös mahdollista tehdä 1600m^2 aitaus esimerkiksi mitolla 799,00 m * 2,002403... m. Tällöin aitaa kuluisi (Piiri) likimain 1602m, eli yli kymmenkertaisesti neliön muotoiseen alueeseen nähden.

Lainaa
ni. 5.7.2016 14:32

Tulos: 0 (16 ääntä)

Mitähän kaavaa Anu käytti...?

Lainaa
Turo 5.7.2016 14:58

Tulos: +46 (52 ääntä)

Mikä ryhmä on kyseessä? Haluan liittyä.

Lainaa
tavis 5.7.2016 21:11

Tulos: +36 (42 ääntä)

Kappas, täytyy tunnustaa et ekaa kertaa feissarimokia lukiessa oppi (muisti hämärästi) jotain uutta (vanhaa). Eipä ole tullut nelosluokan jälkeen vastaan elämässä, et olisi pitänyt pohtia tuota. Aina ollut oleelliset laskukaavan osat saatavilla :)

Lainaa
TapioRautaWaara 5.7.2016 21:49

Tulos: -86 (94 ääntä)

Huoooooh mitä pilkun n*ssintaa. Kaikilla omat alat ja se siitä. Mä oon kokki ja sä oot siivooja. So what?

Lainaa
Hairysteed 5.7.2016 22:04

Tulos: +31 (43 ääntä)

Onko tämä maa muka ollut joskus pisa-tutkimuksen kärjessä?

Lainaa
ookoo 5.7.2016 23:25

Tulos: +23 (35 ääntä)

Ite oisin vaa ottanu mittanauhan käteen ja lähteny mittaamaan. Niinku viimenen ehottikin.

Lainaa
ookoo 5.7.2016 23:26

Tulos: +14 (30 ääntä)

Tai siis mikä mittarulla lie. En siis tarkottanu sitä metrin pituista.

Lainaa
Lendi 6.7.2016 1:15

Tulos: -21 (27 ääntä)

Montako mittarullaa ookoolla sattuu olemaan? Joka kaapissa?

Lainaa
purppurakruunu 6.7.2016 1:30

Tulos: +31 (31 ääntä)

Lendi: Montako mittarullaa ookoolla sattuu olemaan? Joka kaapissa?
Yhden sivun kun olisi askelilla vaikka mitannut, niin olisi saanut ainakin ideaa siihen, paljonko sitä aitaa tarvitaan.

Lainaa
asgasga 6.7.2016 4:24

Tulos: -23 (29 ääntä)

Aidan tarve voi olla myös ääretön, jos alueen pinta-ala on äärettömän pieni.

Lainaa
asgasga 6.7.2016 4:25

Tulos: +20 (24 ääntä)

asgasga: Aidan tarve voi olla myös ääretön, jos alueen pinta-ala on äärettömän pieni.
Ei siis pinta-ala, vaan leveys tai pituus.

Lainaa
Kolhonperä 6.7.2016 8:11

Tulos: +66 (66 ääntä)

KlaaraKotko: Siis.. Oliko se tossa piirustuksessa vaan tuhrinut sinne sisään kuulakärkikynällä kymmenen neliötä.
Siiiiis… Miksi sinä sitä äimistelet?

Lainaa
möö 6.7.2016 19:40

Tulos: +29 (29 ääntä)

Hetken olin samaa mieltä ekan kommentoijan kanssa, noin kuudessa sekunnissa teki mieli facepalmata itselleni. Syytän kesälomaa, aivot on jo kytketty off-asentoon. :D

Lainaa
mau 6.7.2016 21:01

Tulos: +27 (27 ääntä)

"pintaalasta-"

Lainaa
Jorma 7.7.2016 14:13

Tulos: +23 (27 ääntä)

Arthur Brown: Niin, oikeastaan tässä voi antaa vain minimin, joka on noin 140 metriä. Maksimimitta on ääretön, tai no sen verran että avaruuden geometria pysyy vielä jotenkuten järjestyksessä. Jos aidan pituus lähestyy muutamaa miljardia kilometriä, niin aidan massa alkaa jo vaikuttamaan pituusmittaan. Tätä kun jatkaa, niin koko kysymys aidan pituudesta on lähes filosofinen, kun aita ja tontti puristuvat singulariteetiksi. No…oikea vastaus on toki noin 160 metriä (esim. 30 x 50 m tontti).
Tosin kun nyt on puhe reaalielämän objekteista, niin aidalla on oltava paksuus, ja jotta jokin alue voitaisiin aidalla rajata, niin pienin tällainen alue on leveydeltään/pituudeltaan 2 kertaa aidan paksuinen. Sanoisin että realistinen paksuus aidalle on kutakuinkin 1 mm. Jotta aitaus pystyttäisiin suorittamaan, niin tuon alueen oltava siis mitoiltaan vähintään 2mm x 750000m suorakulmio, jolloin aitaa menee 1 500 000,004 metriä. Sanoisin tuota aikalailla maksimiksi.

Lainaa
Mittarimato 8.7.2016 4:24

Tulos: +47 (49 ääntä)

Lendi: Montako mittarullaa ookoolla sattuu olemaan? Joka kaapissa?
Vain yksi. Ainakin minulla. Mutta onneksi sen mittauksen voi toteuttaa silleen jännällä tavalla, että mittaa ensin sen 50 metriä (minkä mittasia nuo nauhat yleensä on) ja pistää merkin paikkaan, johon mitta loppui. Kelaa nauhan ja jatkaa kyseisen merkin kohdalta uudestaa. Uskomatonta eikö?!

Lainaa
Janne 8.7.2016 22:26

Tulos: -39 (45 ääntä)

Eikö neliöjuuri ole ihan perusjuttu kaikille? Sehän on siis nelön juuri, eli yhden sivun pituus. Eli 1500 neliössä sivun pituus on 38.7m kun otetaan neliöjuuri. Sen kun kertoo sivujen määrällä eli neljällä saa kokonaispituuden.

Lainaa
krrp 8.7.2016 22:48

Tulos: +36 (40 ääntä)

Janne: Eikö neliöjuuri ole ihan perusjuttu kaikille? Sehän on siis nelön juuri, eli yhden sivun pituus. Eli 1500 neliössä sivun pituus on 38.7m kun otetaan neliöjuuri. Sen kun kertoo sivujen määrällä eli neljällä saa kokonaispituuden.
Tuo pätee vain jos tontin muoto on neliö. Saija ei koskaan sanonut minkä muotoisesta tontista on kyse, vain sen pinta-alan. Jos tontti on suorakaide tai kolmio tai ympyrä tai fraktaali, tulokseksi voi tulla mitä tahansa 140 metrin ja äärettömän valovuoden väliltä.

Lainaa
Tsooma 8.7.2016 23:51

Tulos: -28 (34 ääntä)

Käytännössä aitaa menee vähiten jos pohjan ala on suurinpiirtein tulitikkuaskin muotoinen. Jos haluaa tehdä talon jossa on pinta-alaan nähden vähän seinää, tuo tulitikkuaskin pohjamalli säästää materiaaleja.

Lainaa
Rajakkisuvakki 9.7.2016 14:14

Tulos: +29 (31 ääntä)

Tsooma: Käytännössä aitaa menee vähiten jos pohjan ala on suurinpiirtein tulitikkuaskin muotoinen. Jos haluaa tehdä talon jossa on pinta-alaan nähden vähän seinää, tuo tulitikkuaskin pohjamalli säästää materiaaleja.

Tsooma: Käytännössä aitaa menee vähiten jos pohjan ala on suurinpiirtein tulitikkuaskin muotoinen. Jos haluaa tehdä talon jossa on pinta-alaan nähden vähän seinää, tuo tulitikkuaskin pohjamalli säästää materiaaleja.
Aivan höpöpuhetta. Ympyränmuotoiseen tonttiin menisi vähiten aitaa, siitä sitten kulmia mukaan niin että aletaan lähestyä neliötä. Neliönmuotoiseen menee vähemmän aitaa kuin mihinkään muuhun suorakulmioon, esim tikkuaskin muotoiseen.

Lainaa
NoloMerete 14.7.2016 23:26

Tulos: +5 (7 ääntä)

Nolo toi Merete. Oli nii varma "voitostaan" xD

Lainaa
Janne 25.7.2016 11:08

Tulos: +7 (9 ääntä)

Raivostuttavaa kun tyhmät tinkaa eivätkä edes tajua olevansa väärässä.

Lainaa
huoh 28.7.2016 23:56

Tulos: -26 (28 ääntä)

tuollahan se sanoo mokassa selkeesti että NELIÖN muotoinen tontti on kyseessä XD. Kommenteille sai taas nauraa eniten

Lainaa
foo 3.8.2016 13:35

Tulos: +23 (23 ääntä)

huoh: tuollahan se sanoo mokassa selkeesti että NELIÖN muotoinen tontti on kyseessä XD. Kommenteille sai taas nauraa eniten
Eikä sano.

Lainaa
Jermu 6.11.2016 14:50

Tulos: +7 (9 ääntä)

Ottakaa huomioon, aita tarvii myös portin, jonka osalta aitaa ei verkoteta

Lainaa
Jaska 6.4.2018 3:15

Tulos: -3 (3 ääntä)

6000 metriä =)

Lainaa
jukkapalmu 30.8.2019 17:24

Tulos: +4 (4 ääntä)

NELIÖN muotoseen menis vähiten, koska siinä on eniten neliöitä mitkä ei "osu" reunaan.

Lainaa
Kirpeä Ahven 5.11.2022 20:45

Tulos: +1 (1 ääni)

Ryusuzaku: Todennäköistä että ensimmäinen osuu oikeaan jos miettii näitä suomen tontteja harvemmin on kauhean kapeita ja pitkiä ainakaan.
Kyllä löytyy. Meillä on pitkän ja kapeahkon kolmion muotoinen.

Lainaa